Within the first publish on this sequence, we launched the usage of hashing methods to detect related features in reverse engineering eventualities. We described PIC hashing, the hashing approach we use in SEI Pharos, in addition to some terminology and metrics to guage how effectively a hashing approach is working. We left off final time after exhibiting that PIC hashing performs poorly in some circumstances, and questioned aloud whether it is attainable to do higher.
On this publish, we’ll attempt to reply that query by introducing and experimenting with a really completely different kind of hashing known as fuzzy hashing. Like common hashing, there’s a hash perform that reads a sequence of bytes and produces a hash. Not like common hashing, although, you do not examine fuzzy hashes with equality. As a substitute, there’s a similarity perform that takes two fuzzy hashes as enter and returns a quantity between 0 and 1, the place 0 means fully dissimilar and 1 means fully related.
My colleague, Cory Cohen, and I debated whether or not there may be utility in making use of fuzzy hashes to instruction bytes, and our debate motivated this weblog publish. I assumed there could be a profit, however Cory felt there wouldn’t. Therefore, these experiments. For this weblog publish, I will be utilizing the Lempel-Ziv Jaccard Distance fuzzy hash (LZJD) as a result of it is quick, whereas most fuzzy hash algorithms are sluggish. A quick fuzzy hashing algorithm opens up the opportunity of utilizing fuzzy hashes to seek for related features in a big database and different fascinating potentialities.
As a baseline I will even be utilizing Levenshtein distance, which is a measure of what number of adjustments it’s essential to make to at least one string to remodel it to a different. For instance, the Levenshtein distance between “cat” and “bat” is 1, since you solely want to alter the primary letter. Levenshtein distance permits us to outline an optimum notion of similarity on the instruction byte stage. The tradeoff is that it is actually sluggish, so it is solely actually helpful as a baseline in our experiments.
Experiments in Accuracy of PIC Hashing and Fuzzy Hashing
To check the accuracy of PIC hashing and fuzzy hashing underneath numerous eventualities, I outlined a number of experiments. Every experiment takes an analogous (or equivalent) piece of supply code and compiles it, typically with completely different compilers or flags.
Experiment 1: openssl model 1.1.1w
On this experiment, I compiled openssl model 1.1.1w in a number of alternative ways. In every case, I examined the ensuing openssl executable.
Experiment 1a: openssl1.1.1w Compiled With Totally different Compilers
On this first experiment, I compiled openssl 1.1.1w with gcc -O3 -g and clang -O3 -g and in contrast the outcomes. We’ll begin with the confusion matrix for PIC hashing:
|
|
|
|
|
|
|
|
|
|
|
|
As we noticed earlier, this leads to a recall of 0.07, a precision of 0.45, and a F1 rating of 0.12. To summarize: fairly dangerous.
How do LZJD and Levenshtein distance do? Effectively, that is a bit tougher to quantify, as a result of we’ve to choose a similarity threshold at which we take into account the perform to be “the identical.” For instance, at a threshold of 0.8, we would take into account a pair of features to be the identical if that they had a similarity rating of 0.8 or larger. To speak this info, we might output a confusion matrix for every attainable threshold. As a substitute of doing this, I will plot the outcomes for a spread of thresholds proven in Determine 1 under:
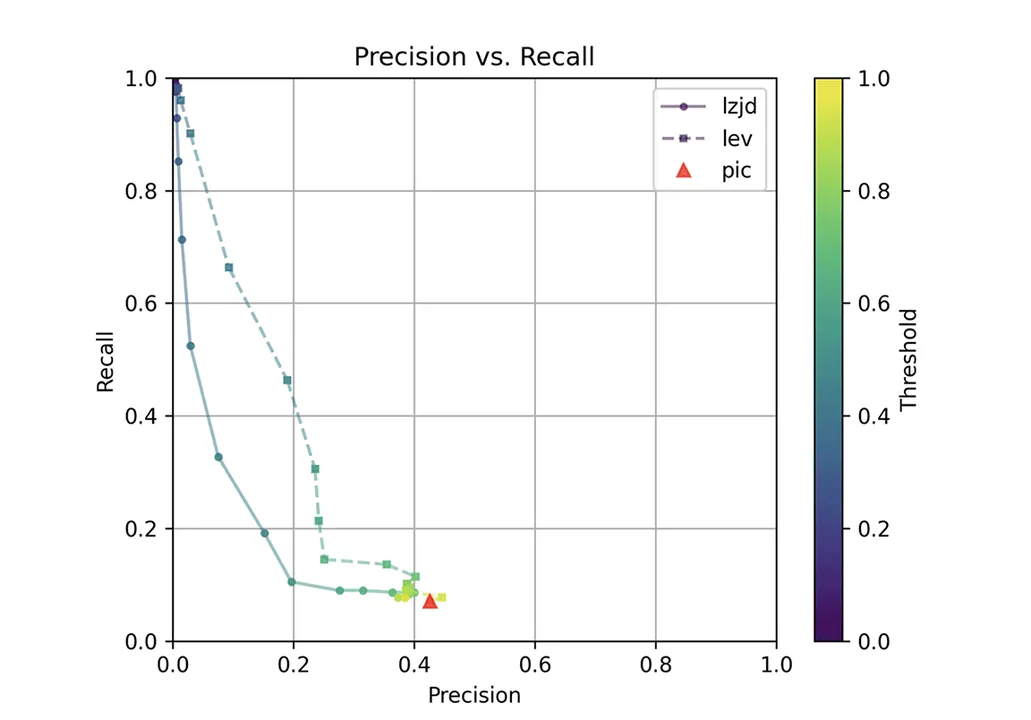
Determine 1: Precision Versus Recall Plot for “openssl GCC vs. Clang”
The purple triangle represents the precision and recall of PIC hashing: 0.45 and 0.07 respectively, identical to we calculated above. The strong line represents the efficiency of LZJD, and the dashed line represents the efficiency of Levenshtein distance (LEV). The colour tells us what threshold is getting used for LZJD and LEV. On this graph, the perfect outcome could be on the high proper (100% recall and precision). So, for LZJD and LEV to have a bonus, it must be above or to the best of PIC hashing. However, we are able to see that each LZJD and LEV go sharply to the left earlier than transferring up, which signifies {that a} substantial lower in precision is required to enhance recall.
Determine 2 illustrates what I name the violin plot. Chances are you’ll need to click on on it to zoom in. There are three panels: The leftmost is for LEV, the center is for PIC hashing, and the rightmost is for LZJD. On every panel, there’s a True column, which exhibits the distribution of similarity scores for equal pairs of features. There’s additionally a False column, which exhibits the distribution scores for nonequivalent pairs of features. Since PIC hashing doesn’t present a similarity rating, we take into account each pair to be both equal (1.0) or not (0.0). A horizontal dashed line is plotted to point out the edge that has the best F1 rating (i.e., a very good mixture of each precision and recall). Inexperienced factors point out perform pairs which are accurately predicted as equal or not, whereas purple factors point out errors.
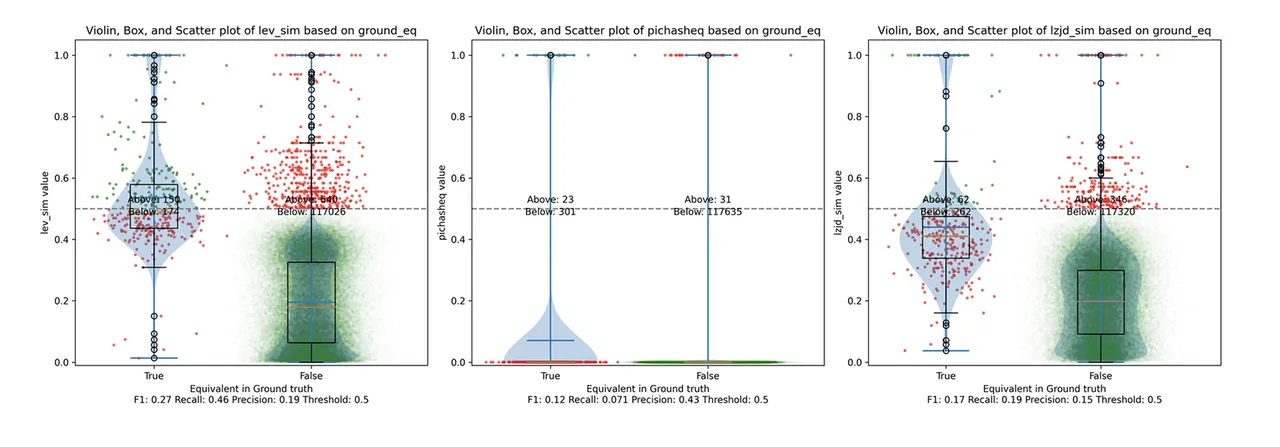
Determine 2: Violin Plot for “openssl gcc vs clang”. Click on to zoom in.
This visualization exhibits how effectively every similarity metric differentiates the similarity distributions of equal and nonequivalent perform pairs. Clearly, the hallmark of a very good similarity metric is that the distribution of equal features must be larger than nonequivalent features. Ideally, the similarity metric ought to produce distributions that don’t overlap in any respect, so we might draw a line between them. In follow, the distributions normally intersect, and so as an alternative we’re pressured to make a tradeoff between precision and recall, as could be seen in Determine 1.
Total, we are able to see from the violin plot that LEV and LZJD have a barely larger F1 rating (reported on the backside of the violin plot), however none of those methods are doing a fantastic job. This suggests that gcc and clang produce code that’s fairly completely different syntactically.
Experiment 1b: openssl 1.1.1w Compiled With Totally different Optimization Ranges
The following comparability I did was to compile openssl 1.1.1w with gcc -g and optimization ranges -O0, -O1, -O2, -O3.
Evaluating Optimization Ranges -O0 and -O3
Let’s begin with one of many extremes, evaluating -O0 and -O3:
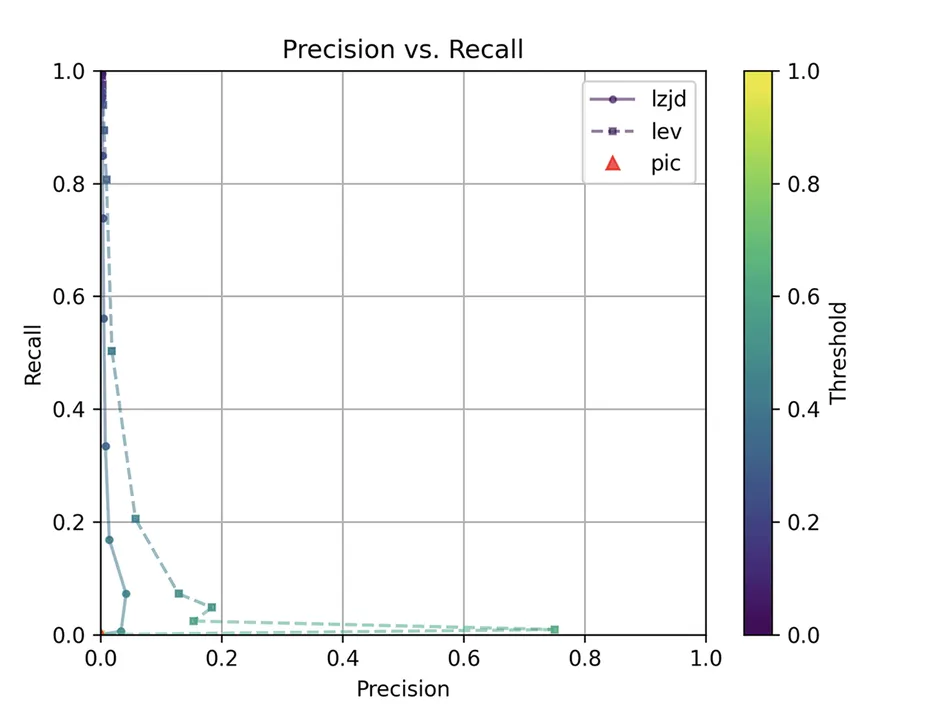
Determine 3: Precision vs. Recall Plot for “openssl -O0 vs -O3”
The very first thing you may be questioning about on this graph is, The place is PIC hashing? Effectively, in the event you look carefully, it is there at (0, 0). The violin plot offers us just a little extra details about what’s going on.
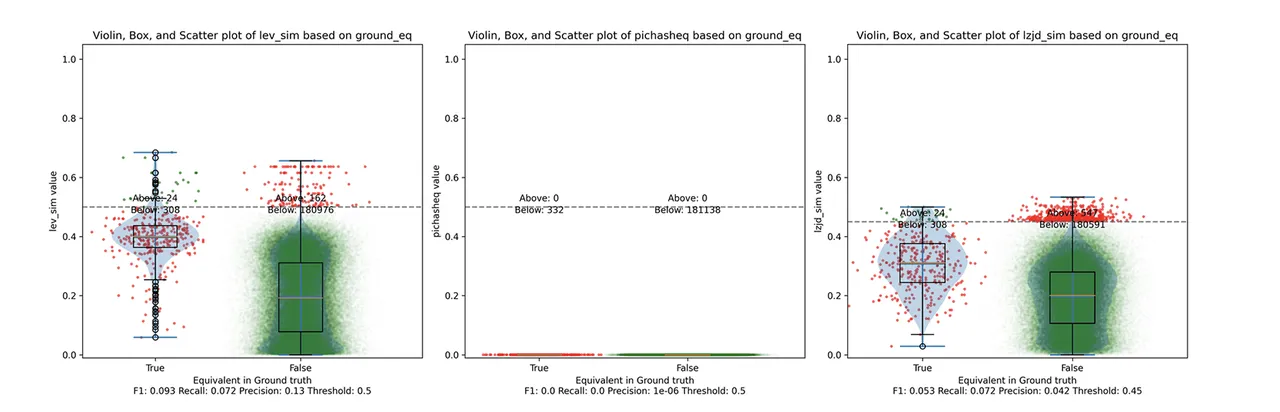
Determine 4: Violin Plot for “openssl -O0 vs -O3”. Click on to zoom in.
Right here we are able to see that PIC hashing made no constructive predictions. In different phrases, not one of the PIC hashes from the -O0 binary matched any of the PIC hashes from the -O3 binary. I included this experiment as a result of I assumed it will be very difficult for PIC hashing, and I used to be proper. However, after some dialogue with Cory, we realized one thing fishy was occurring. To realize a precision of 0.0, PIC hashing cannot discover any features equal. That features trivially easy features. In case your perform is only a ret there’s not a lot optimization to do.
Ultimately, I guessed that the -O0 binary didn’t use the -fomit-frame-pointer possibility, whereas all different optimization ranges do. This issues as a result of this selection adjustments the prologue and epilogue of each perform, which is why PIC hashing does so poorly right here.
LEV and LZJD do barely higher once more, reaching low (however nonzero) F1 scores. However to be honest, not one of the methods do very effectively right here. It is a troublesome downside.
Evaluating Optimization Ranges -O2 and -O3
On the a lot simpler excessive, let us take a look at -O2 and -O3.
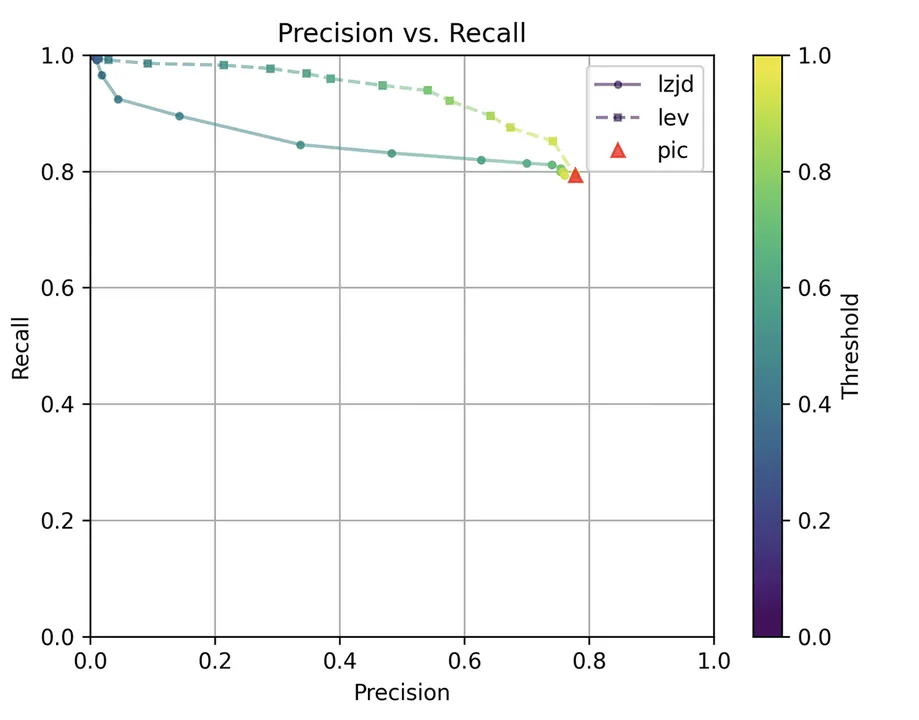
Determine 5: Precision vs. Recall Plot for “openssl -O2 vs -O3”
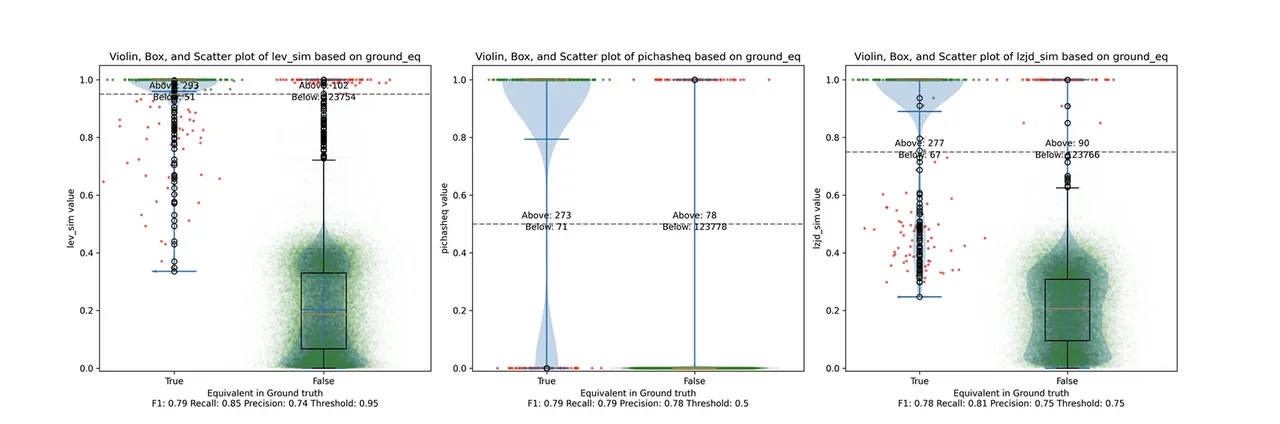
Determine 6: Violin Plot for “openssl -O1 vs -O2”. Click on to zoom in.
PIC hashing does fairly effectively right here, reaching a recall of 0.79 and a precision of 0.78. LEV and LZJD do about the identical. Nevertheless, the precision vs. recall graph (Determine 11) for LEV exhibits a way more interesting tradeoff line. LZJD’s tradeoff line is just not practically as interesting, because it’s extra horizontal.
You can begin to see extra of a distinction between the distributions within the violin plots right here within the LEV and LZJD panels. I will name this one a three-way “tie.”
Evaluating Optimization Ranges -O1 and -O2
I might additionally count on -O1 and -O2 to be pretty related, however not as related as -O2 and -O3. Let’s examine:
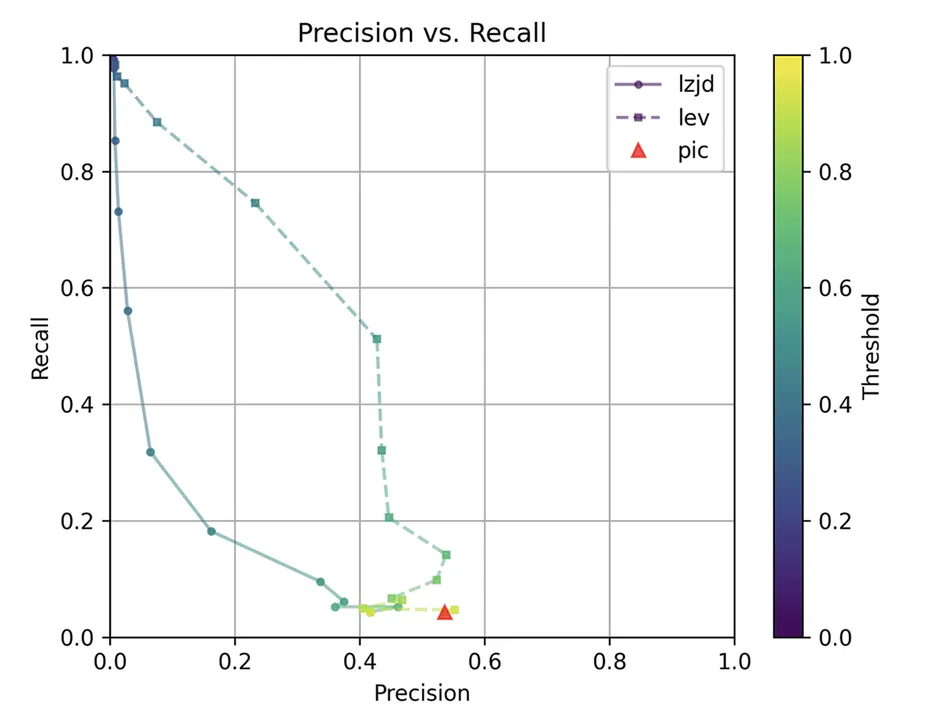
Determine 7: Precision vs. Recall Plot for “openssl -O1 vs -O2”
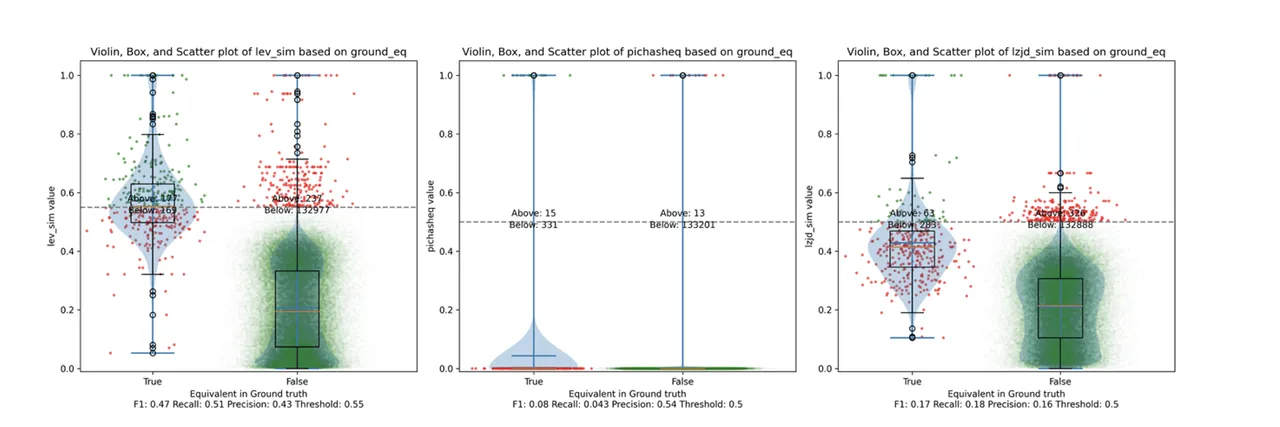
Determine 8: Violin Plot for “openssl -O1 vs -O2”. Click on to zoom in.
The precision vs. recall graph (Determine 7) is sort of fascinating. PIC hashing begins at a precision of 0.54 and a recall of 0.043. LEV shoots straight up, indicating that by reducing the edge it’s attainable to extend recall considerably with out dropping a lot precision. A very engaging tradeoff may be a precision of 0.43 and a recall of 0.51. That is the kind of tradeoff I hoped to see with fuzzy hashing.
Sadly, LZJD’s tradeoff line is once more not practically as interesting, because it curves within the incorrect route.
We’ll say this can be a fairly clear win for LEV.
Evaluating Optimization Ranges -O1 and -O3
Lastly, let’s examine -O1 and -O3, that are completely different, however each have the -fomit-frame-pointer possibility enabled by default.
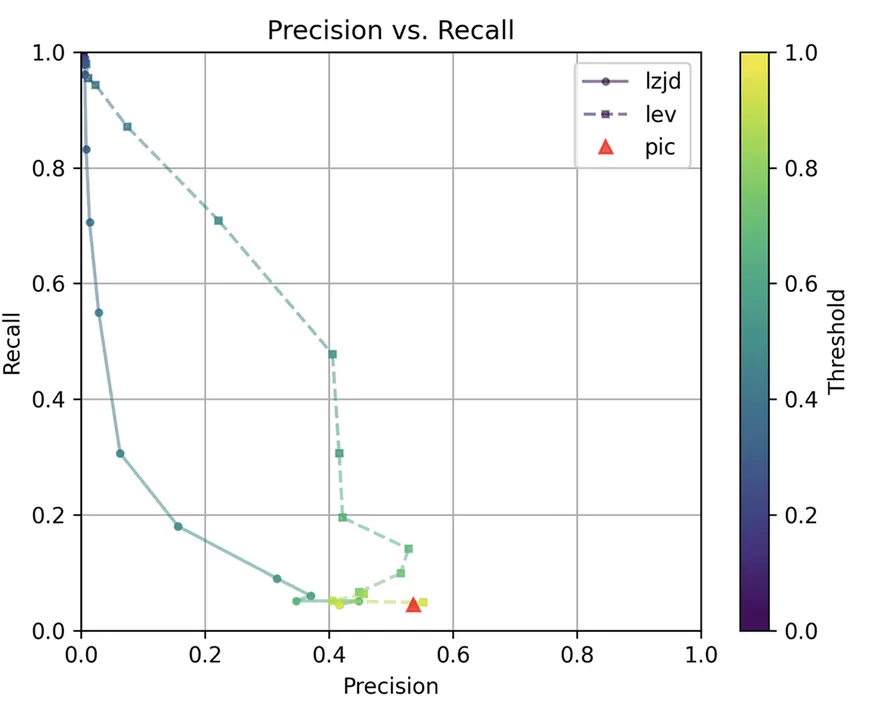
Determine 9: Precision vs. Recall Plot for “openssl -O1 vs -O3”
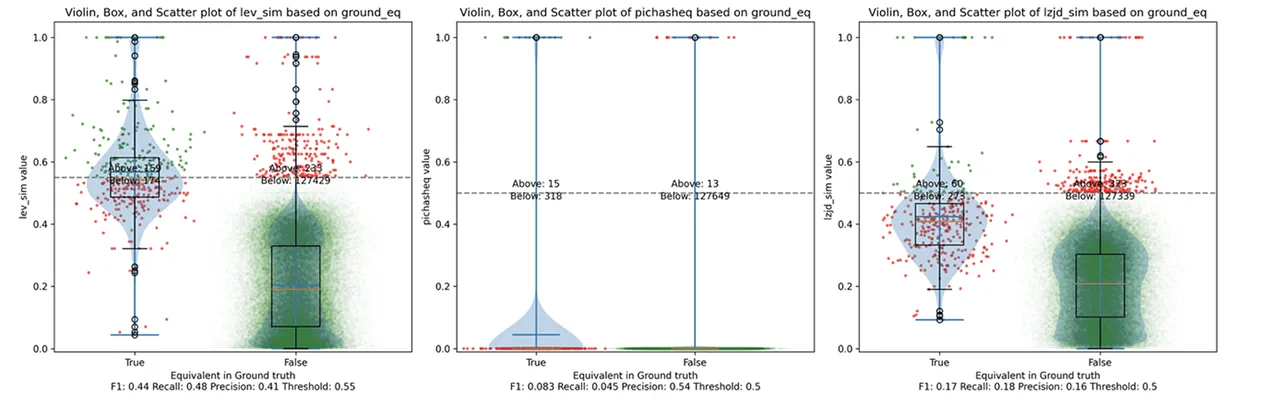
Determine 10: Violin Plot for “openssl -O1 vs -O3”. Click on to zoom in.
These graphs look nearly equivalent to evaluating -O1 and -O2. I might describe the distinction between -O2 and -O3 as minor. So, it is once more a win for LEV.
Experiment 2: Totally different openssl Variations
The ultimate experiment I did was to match numerous variations of openssl. Cory instructed this experiment as a result of he thought it was reflective of typical malware reverse engineering eventualities. The thought is that the malware writer launched Malware 1.0, which you reverse engineer. Later, the malware adjustments a number of issues and releases Malware 1.1, and also you need to detect which features didn’t change in an effort to keep away from reverse engineering them once more.
I in contrast a number of completely different variations of openssl:
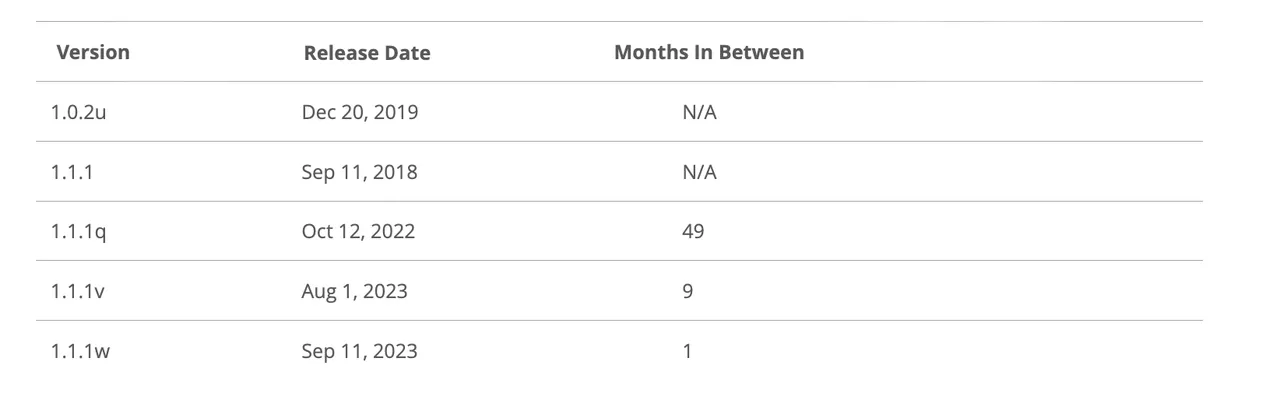
I compiled every model utilizing gcc -g -O2.
openssl 1.0 and 1.1 are completely different minor variations of openssl. As defined right here:
Letter releases, comparable to 1.0.2a, solely include bug and safety fixes and no new options.
So, we’d count on that openssl 1.0.2u is pretty completely different from any 1.1.1 model. And, we’d count on that in the identical minor model, 1.1.1 could be much like 1.1.1q, however it will be extra completely different than 1.1.1w.
Experiment 2a: openssl 1.0.2u vs 1.1.1w
As earlier than, let’s begin with essentially the most excessive comparability: 1.0.2u vs 1.1.1w.
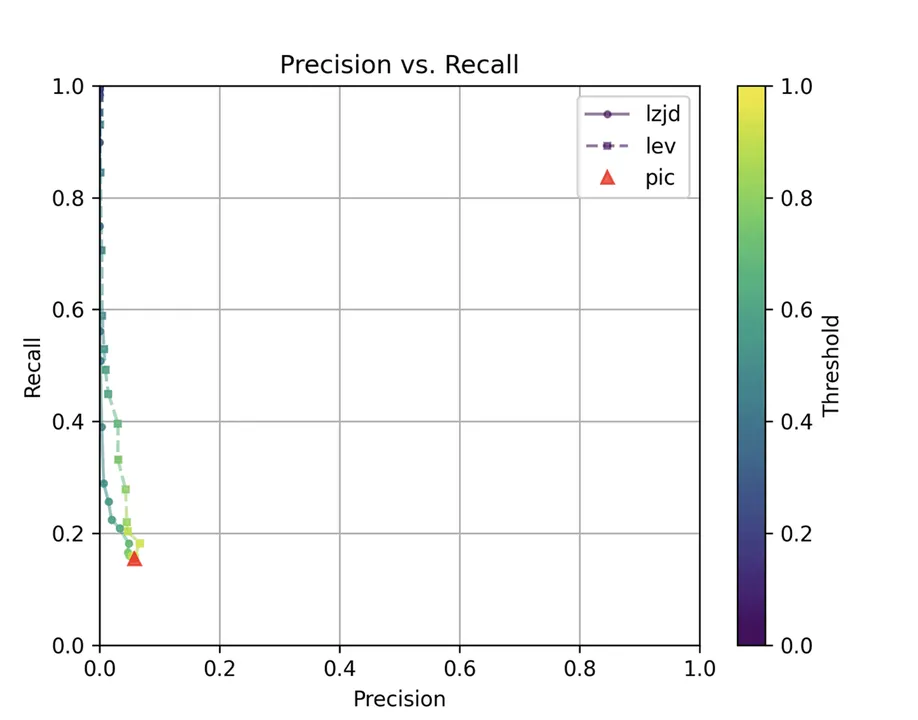
Determine 11: Precision vs. Recall Plot for “openssl 1.0.2u vs 1.1.1w”
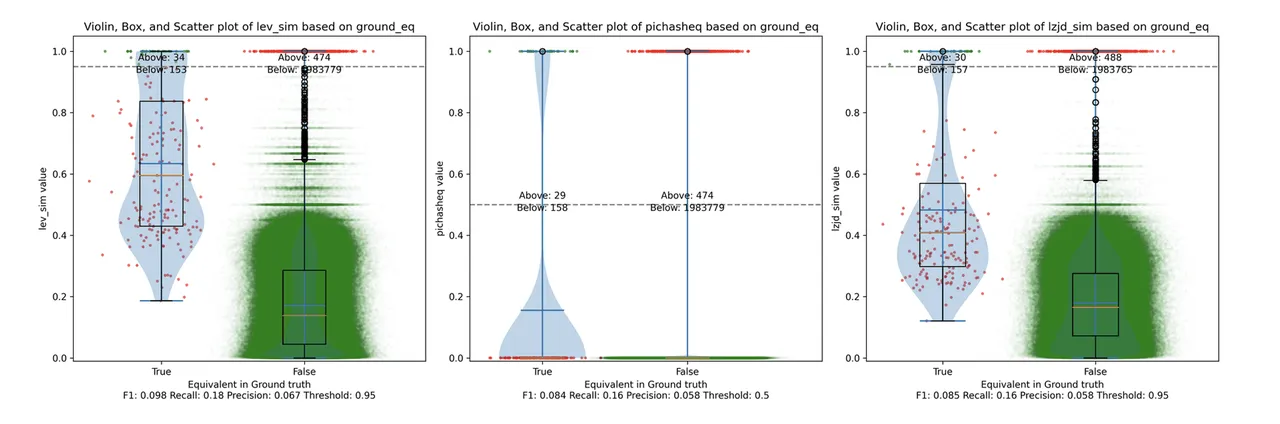
Determine 12: Violin Plot for “openssl 1.0.2u vs 1.1.1w”. Click on to zoom in.
Maybe not surprisingly, as a result of the 2 binaries are fairly completely different, all three methods wrestle. We’ll say this can be a three approach tie.
Experiment 2b: openssl 1.1.1 vs 1.1.1w
Now, let us take a look at the unique 1.1.1 launch from September 2018 and examine it to the 1.1.1w bugfix launch from September 2023. Though a whole lot of time has handed between the releases, the one variations must be bug and safety fixes.
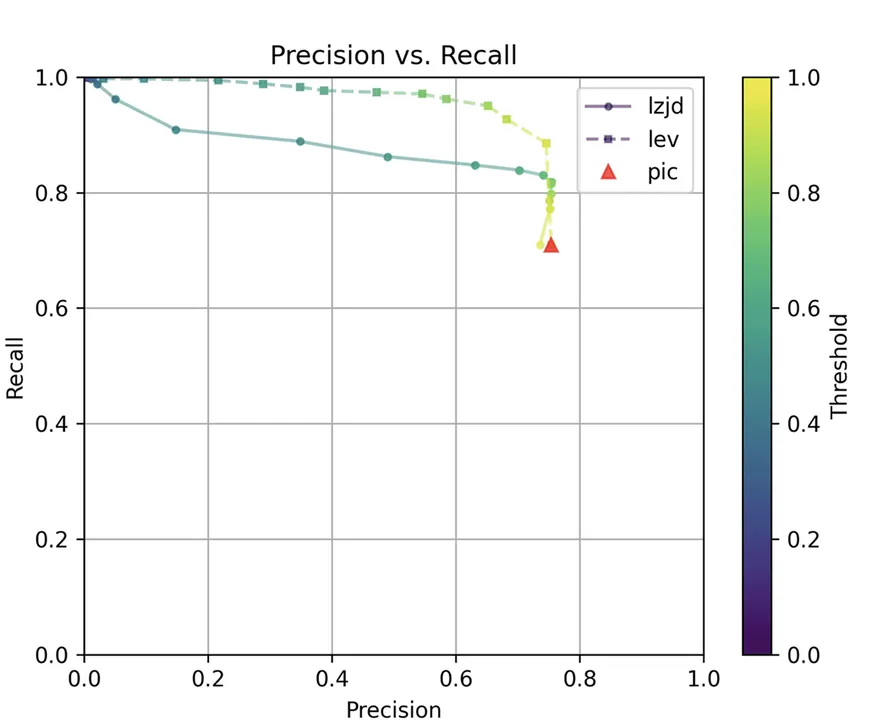
Determine 13: Precision vs. Recall Plot for “openssl 1.1.1 vs 1.1.1w”
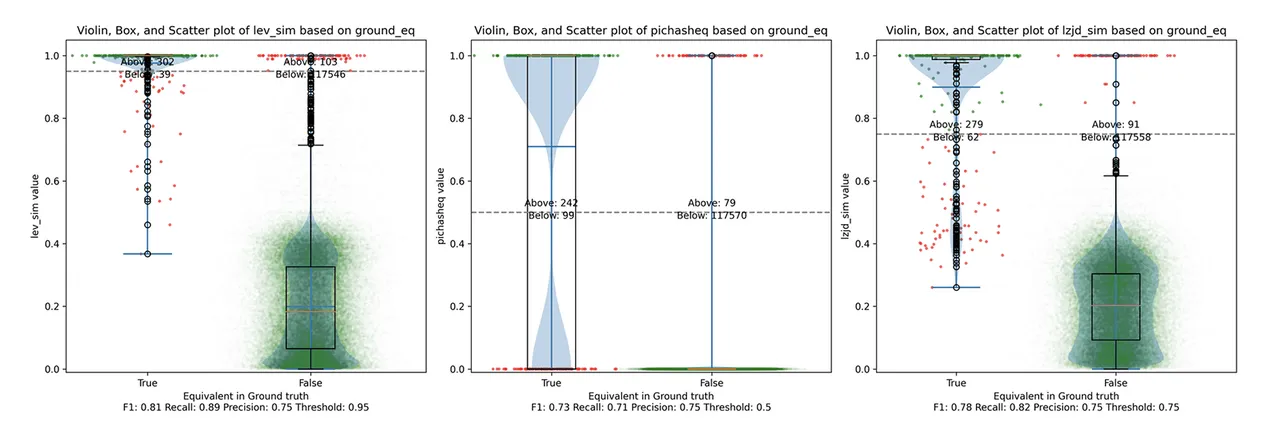
Determine 14: Violin Plot for “openssl 1.1.1 vs 1.1.1w”. Click on to zoom in.
All three methods do significantly better on this experiment, presumably as a result of there are far fewer adjustments. PIC hashing achieves a precision of 0.75 and a recall of 0.71. LEV and LZJD go nearly straight up, indicating an enchancment in recall with minimal tradeoff in precision. At roughly the identical precision (0.75), LZJD achieves a recall of 0.82 and LEV improves it to 0.89. LEV is the clear winner, with LZJD additionally exhibiting a transparent benefit over PIC.
Experiment 2c: openssl 1.1.1q vs 1.1.1w
Let’s proceed taking a look at extra related releases. Now we’ll examine 1.1.1q from July 2022 to 1.1.1w from September 2023.
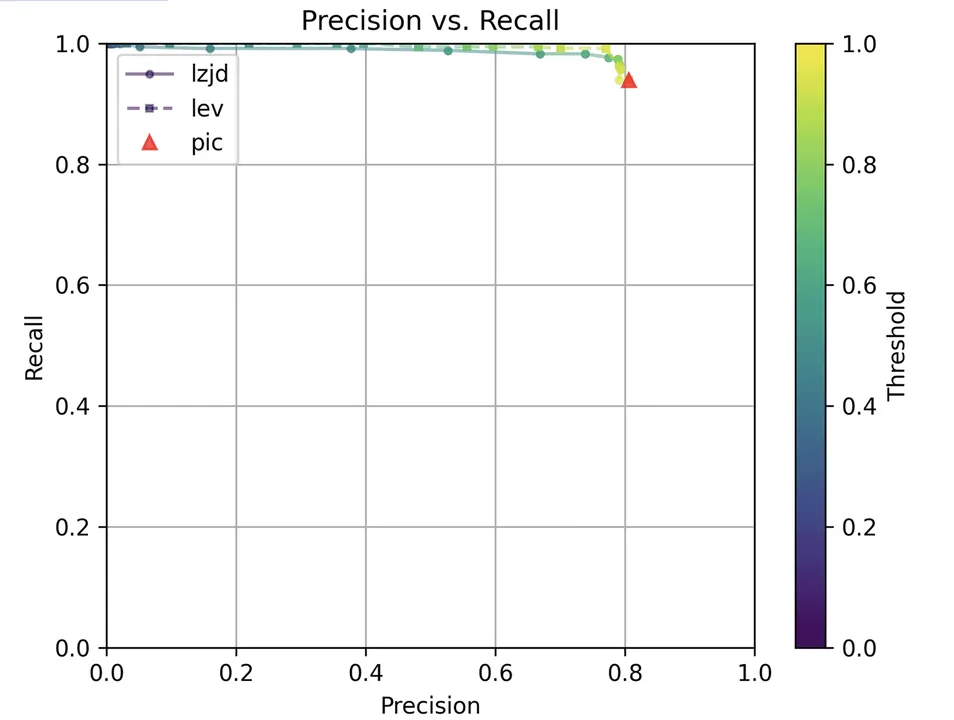
Determine 15: Precision vs. Recall Plot for “openssl 1.1.1q vs 1.1.1w”
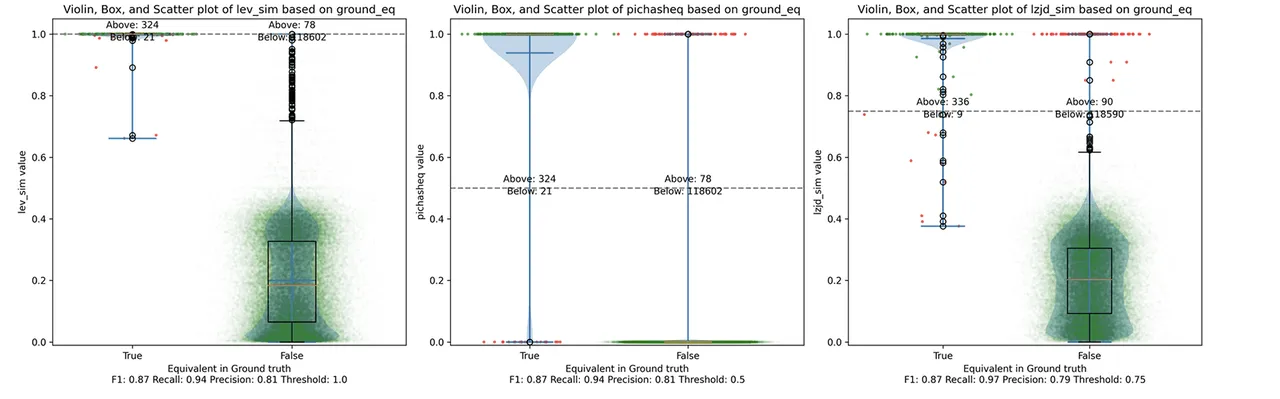
Determine 16: Violin Plot for “openssl 1.1.1q vs 1.1.1w”. Click on to zoom in.
As could be seen within the precision vs. recall graph (Determine 15), PIC hashing begins at a formidable precision of 0.81 and a recall of 0.94. There merely is not a whole lot of room for LZJD or LEV to make an enchancment. This leads to a three-way tie.
Experiment second: openssl 1.1.1v vs 1.1.1w
Lastly, we’ll take a look at 1.1.1v and 1.1.1w, which had been launched solely a month aside.
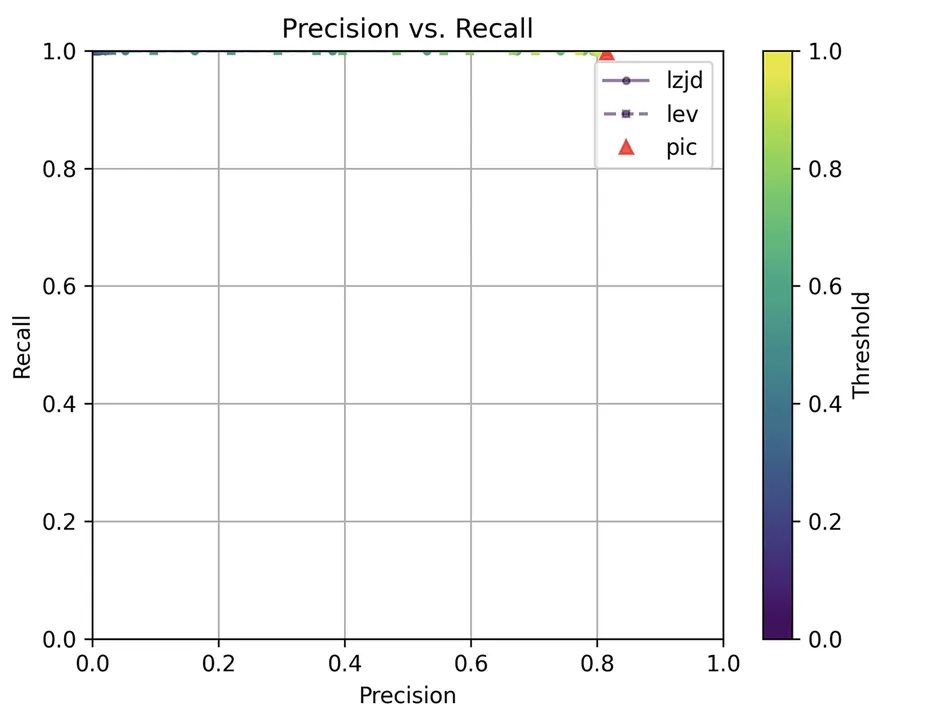
Determine 17: Precision vs. Recall Plot for “openssl 1.1.1v vs 1.1.1w”
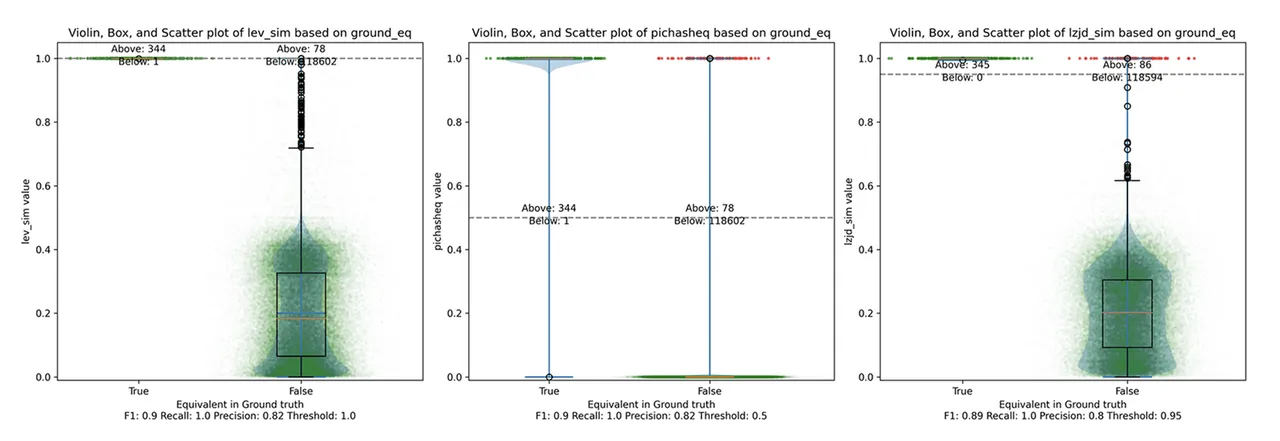
Determine 18: Violin Plot for “openssl 1.1.1v vs 1.1.1w”. Click on to zoom in.
Unsurprisingly, PIC hashing does even higher right here, with a precision of 0.82 and a recall of 1.0 (after rounding). Once more, there’s principally no room for LZJD or LEV to enhance. That is one other three approach tie.
Conclusions: Thresholds in Observe
We noticed some eventualities by which LEV and LZJD outperformed PIC hashing. Nevertheless, it is necessary to comprehend that we’re conducting these experiments with floor reality, and we’re utilizing the bottom reality to pick the optimum threshold. You’ll be able to see these thresholds listed on the backside of every violin plot. Sadly, in the event you look fastidiously, you may additionally discover that the optimum thresholds will not be all the time the identical. For instance, the optimum threshold for LZJD within the “openssl 1.0.2u vs 1.1.1w” experiment was 0.95, nevertheless it was 0.75 within the “openssl 1.1.1q vs 1.1.1w” experiment.
In the actual world, to make use of LZJD or LEV, it’s essential to choose a threshold. Not like in these experiments, you may not choose the optimum one, since you would don’t have any approach of realizing in case your threshold was working effectively or not. If you happen to select a poor threshold, you would possibly get considerably worse outcomes than PIC hashing.
PIC Hashing is Fairly Good
I believe we discovered that PIC hashing is fairly good. It isn’t good, nevertheless it usually supplies glorious precision. In concept, LZJD and LEV can carry out higher by way of recall, which is interesting. In follow, nonetheless, it will not be clear that they might as a result of you wouldn’t know which threshold to make use of. Additionally, though we did not discuss a lot about computational efficiency, PIC hashing may be very quick. Though LZJD is a lot quicker than LEV, it is nonetheless not practically as quick as PIC.
Think about you could have a database of 1,000,000 malware perform samples and you’ve got a perform that you just need to search for within the database. For PIC hashing, that is simply an ordinary database lookup, which might profit from indexing and different precomputation methods. For fuzzy hash approaches, we would wish to invoke the similarity perform 1,000,000 occasions every time we needed to do a database lookup.
There is a Restrict to Syntactic Similarity
Keep in mind that we included LEV to symbolize the optimum similarity primarily based on the edit distance of instruction bytes. LEV didn’t considerably outperform PIC , which is sort of telling, and suggests that there’s a basic restrict to how effectively syntactic similarity primarily based on instruction bytes can carry out. Surprisingly, PIC hashing seems to be near that restrict. We noticed a placing instance of this restrict when the body pointer was unintentionally omitted and, extra usually, all syntactic methods wrestle when the variations turn into too nice.
It’s unclear whether or not any variants, like computing similarities over meeting code as an alternative of executable code bytes, would carry out any higher.
The place Do We Go From Right here?
There are after all different methods for evaluating similarity, comparable to incorporating semantic info. Many researchers have studied this. The final draw back to semantic methods is that they’re considerably costlier than syntactic methods. However, in the event you’re prepared to pay the upper computational worth, you may get higher outcomes.
Just lately, a serious new characteristic known as BSim was added to Ghidra. BSim can discover structurally related features in doubtlessly massive collections of binaries or object information. BSim relies on Ghidra’s decompiler and may discover matches throughout compilers used, architectures, and/or small adjustments to supply code.
One other fascinating query is whether or not we are able to use neural studying to assist compute similarity. For instance, we would be capable of practice a mannequin to grasp that omitting the body pointer doesn’t change the that means of a perform, and so should not be counted as a distinction.
